Dalam matematika, pemrograman linear ialah teknik optimisasi yang melibatkan variabel-variabel linear. Dalam model pemrograman linear dikenal dua macam fungsi, yaitu fungsi objektif (objective function) dan fungsi kendala (constraint function) yang linear.
Pemrograman linear dapat direpresentasikan dalam notasi matematis sebagai berikut:
- Maksimalkan
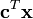
- dengan syarat
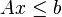
- dan
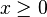
Dalam hal ini, x ialah vektor variabel, sedangkan c dan b ialah vektor koefisien dan A ialah matriks koefisien. Fungsi objektifnya ialah ekspresi yang hendak dimaksimalkan atau diminimalkan (yaitu cTx). Persamaan Ax ≤ b ialah fungsi kendala yang menunjukkan polihedron konveks tempat fungsi objektifnya dioptimisasi.
Pemrograman linear dapat diterapkan pada berbagai bidang studi. Metode ini paling banyak digunakan dalam bisnis danekonomi, namun juga dapat dimanfaatkan dalam sejumlah perhitungan ilmu teknik. Misalnya, dalam ekonomi, fungsi tujuan dapat berkaitan dengan pengaturan secara optimal sumber-sumber daya untuk memperoleh keuntungan maksimal atau biaya minimal, sedangkan fungsi batasan menggambarkan batasan-batasan kapasitas yang tersedia yang dialokasikan secara optimal ke berbagai kegiatan. Industri yang memanfaatkan pemrograman linear di antaranya ialah industri transportasi, energi, telekomunikasi, dan manufaktur. Pemrograman linear juga terbukti berguna dalam membuat model berbagai jenis masalah dalam perencanaan, perancangan rute, penjadwalan, pemberian tugas, dan desain.


Tidak ada komentar:
Posting Komentar